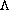FOPI A Detector for the Physics
of Nuclear Reactions

Nuclear matter, of which atomic nuclei are composed, is a system of strongly interacting particles called nucleons. In its ground state, it behaves in a manner analogous to a fluid, and strongly resists attempts at compression. To double the density of nuclear matter, for example, requires 2x10³³ Pascals, a pressure equivalent to twenty times the mass of the earth resting on an area one square millimeter in size. However, a compressed state is required before some of the fundamental properties of nuclear matter reveal themselves. New studies have shown that it is possible, and perhaps even likely, that the properties of the constituents vary according to the density of their surrounding environment. Referring to this phenomenon, scientists talk of a so-called "in-medium effect." The properties of these constituents-elementary particles-are well-known when the particles are surrounded by vacuum. However, their masses may vary due to a particular symmetry of the fundamental interaction-the chiral symmetry of Quantum Chromodynamics. In general, such a supposition is true for all hadrons, i.e. particles subject to the strong interaction. Detecting and understanding the processes at work here should help physicists tackle one of the central problems of modern physics-the inability of theoretical physics to provide an explanation of the principle determining the masses of the elementary particles.

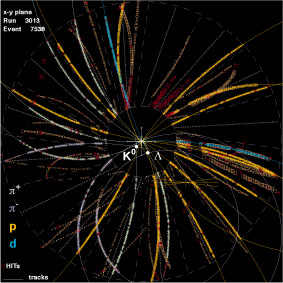
Figure 1: The charged particles produced by a nickel-nickel collision at an energy of 1.93 GeV per nucleon leave tracks in the central drift chamber. The individual signals in the detector (squares) are automatically connected to form the track. Unambiguous identification of the particle is possible from the curvature of the track and additional information from other sections of the FOPI detector. In the example shown, two strange particles (K⁰ and 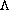) arise simultaneously and decay after a short flight.

Tracking down this kind of behavior, however, requires the investment of considerable effort. Another problem is presented by the fact that not all particles behave in the same way. One group of theoretically-promising candidates is provided by the kaons, which are distinguished by the fact that they contain a strange quark or antiquark. Kaons, however, are relatively difficult to generate in compressed nuclear matter, which in the laboratory can only be created in relativistic heavy-ion collisions, and then only for a relatively short time. For example, twice normal density is achieved in the collision of heavy ions (gold against gold) at an injection energy of around 1 GeV per nucleon, i.e. at an energy where the kinetic energy is almost equal to the rest mass of the nucleon. In this case, the velocity is 267000 km/s or 89 percent of the velocity of light. Within 10^-22 seconds of the impact, the action is all over. All that remains are the fragments, and possibly particles newly-created during the reaction. An analysis of these remnants provides the basis for a reconstruction of the reaction. In addition, these observations reveal that the density in the heavy-ion reaction is also dependent on other quantities. During the attempt to compress nuclei together, part of the energy applied is inevitably converted into disordered motion, i.e. the system is heated. This thermal motion also generates pressure, so that in general, there is an overall relationship between pressure, density, and temperature. Analogous to classical thermodynamics, this relationship is referred to as an equation of state. Exact knowledge of this equation is a precondition for the characterization of the conditions present during the heavy-ion collision. The search for "in-medium properties" will only be successful if sufficient exact knowledge of the surrounding conditions is available. It is thus immediately obvious that the more completely the remnants of the reaction can be measured, the better this search can proceed.

The FOPI Detector

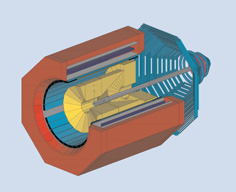
The FOPI detector has documented the investigation of the fragments and the particles produced in central heavy-ion collisions. As suggested by the name - FOPI stands for 4; a synonym for the entire solid angle-this detector detects, identifies, and determines the momentum of all charged particles emitted in a heavy-ion reaction. The detector structure is shown schematically in the diagram. Based on the modular combination of different detector systems, the total assembly achieves its goal of covering the complete range of beam energies (0.1 - 2 GeV per nucleon) made available by GSI's SIS heavy ion synchrotron. The target is located within a superconducting coil, which produces a magnetic field of 0.6 Tesla. Charged particles within this field travel along curved paths before passing through the drift chambers (shown in yellow). These chambers register both the particle track and the energy loss sustained by the particle in its passage through the detector gas. The energy loss is dependent on the type of particle and its momentum in a characteristic way. Figure 1 gives an impression of the available information. This shows the signals ("hits") as squares in a plane normal to the beam axis. In addition, lines have been drawn through connected hits, which have been recognized by the automatic track-recognition of the event. Further on through the detector, the majority of the particles land in scintillation counters (shown blue in the diagram), with which their flight time from the target can be determined. The combination of different measurements enables the unambiguous identification of the particles.

The FOPI detector's potential ability to identify particles is, however, not restricted to charged particles. Although neutral particles do not themselves leave signals in the detector system, some of them can be recognized and reconstructed thanks to their decay. This interesting class of particles includes neutral particles containing a strange quark, such as the neutral kaon and the 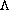-particle. Due to their strangeness, they are relatively long-lived, decaying after a flight of several centimeters into charged particles, which leave tracks in the detectors. Two such decays, also from a nickel-nickel reaction at 1.93 GeV per nucleon, are visible in Figure 1. It can be seen that not all of the tracks originate from the same point. The point of intersection of the majority of tracks is the interaction point in the target. The other tracks are candidates for secondary decays. As the momenta and particle types are already known, the calculation of the invariant masses and comparison with the rest masses of the candidate particles enables the direct determination of which tracks belong together.

Heavy-Ion Reaction Physics

The FOPI detector can simultaneously detect all the charged and some of the neutral particles produced in a heavy-ion reaction. Global correlations among the particles are thus possible. Also known as collective effects, these correlations provide meaningful signatures for the material properties described above. Here, the common properties shared by the various particles emitted are sought in order to reveal the driving forces. Two recent results have attracted particular attention: collective expansion and directed sidewards flow at the highest energies, the latter of which provides interesting information, particularly in the case of strange particles, on interactions with the surrounding matter.

Collective Expansion

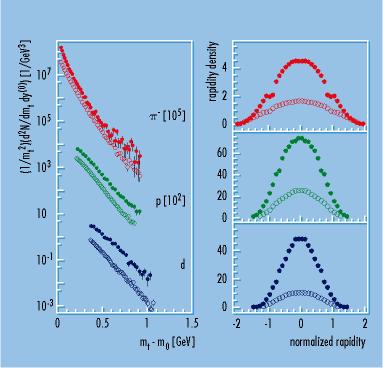
Figure 2: Spectra of the transverse mass (left-hand side) and of the rapidity-density distributions extrapolated over the full range of the transverse momentum region (right-hand side) are shown for the systems gold against gold (solid circles) and nickel against nickel (circles) at an injection energy of 1.06 GeV per nucleon. The collective expansion can be recognized in the systematic variation of the slope of the spectra of the transverse mass (left). Just like the mutual stopping of the nuclei, for which the width of the rapidity-density distribution (right) represents one measure, the expansion depends on the size of the system.

Figure 2 shows one example of the information available to physicists. Essentially, the momentum distributions of the particles are measured. Components in the directions normal to the beam axis are of particular interest, as they are first produced in the reaction. The figure shows spectra of the so-called transverse masses for the reactions nickel against nickel and gold against gold at 1 GeV per nucleon. The transverse mass is derived from the addition of the squares of the rest masses of the respective particle types and their transverse momentum. The spectrum falls off exponentially, although the slope parameters increase with increasing particle mass and system size. The spectra are plotted so that the slope corresponds exactly to the reciprocal of the temperature. Figure 2 could thus mean that the temperatures at which the different particles are produced increase with increasing mass. This hypothesis is ruled out since then the pions would have to be first produced in the reaction and thus would come from its coldest phase. The key to understanding the process lies in the linear dependence of the temperature on the mass of the particles. The mean kinetic energies per particle mass contain a common component for all particles, independently of whether the particle was first produced during the reaction or the constituents were already present before the start of the reaction. Similar observations have been made over a wide range of fragment masses at lower energies using the FOPI detector [1]. This behavior has been interpreted to mean that the observed fragments arise from an expanding flow of matter, from which they all carry the same velocity component into the detector. The magnitude of this collective velocity is astoundingly high. Quantitative investigations show that, as the strong interaction "freezes out," the matter is traveling with a mean velocity of one-third that of light. Naturally, since the energy bound up in the collective kinetic energy is not available to heat the matter, this has consequences for the temperature to which it is heated. Exact analysis for beam energies of 1 GeV per nucleon gives temperatures of 85 MeV, which corresponds to around 10¹² degrees Celcius. Although the density is not directly accessible from the measurements, comparison of the spectra and the rapidity-density distribution (right-hand column, Figure 2) can be used with the predictions of so-called transport models to determine the change in the density over time and the maximum density reached. The rapidity is thus a measure of the velocity component along the direction of the beam. For heavy systems, an beam energy of 1 GeV per nucleon produces approximately double the density of the ground state, and can thus be used at the GSI's SIS heavy ion synchrotron to prepare the conditions specified in the introduction. Variation of the beam energy and of the projectile-target combination enables the region between one and 2.5 times normal density to be covered.

Directed Sidewards Flow

The most intensively discussed theme recently has been the question of how generated particles, in particular vector mesons and kaons, behave under conditions of high temperature and density. It would appear that the observed probabilities of production of the antikaons in particular can currently only described theoretically if it is assumed that particle masses are lower in-medium. Another window on possible "in-medium properties" of kaons is founded upon the directed sidewards flow discovered some fifteen years ago by the GSI/LBL group at the Bevalac. As nuclear matter is extremely difficult to compress, the particles attempt, so far as is possible, to get out of the way. In the case of not completely central collisions-the most probable sort, due to the geometry-the particles are collectively deflected from the collision axis and thus define a preferred direction, which, together with the beam direction, defines the so-called reaction plane. Figure 3 shows how this behavior is reflected in distributions. The momentum components normal to the beam direction are projected onto the reaction plane and then evaluated. This average value is plotted against the rapidity for the various particles. For protons, which are represented by the stepped, green histogram, it can be seen that the average value increases in line with the absolute value of the longitudinal velocity, i.e. the protons are preferentially emitted at a particular angle in the reaction plane. The highest matter density is to be found in this direction.

Mass Resolution

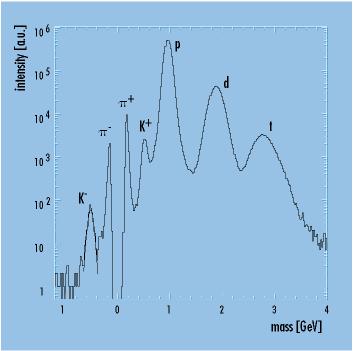
The resolutions possible with the FOPI detector can best be gauged using the mass distributions shown. There, the reconstructed masses are shown for singly-charged particles from the nickel-nickel reaction at 1.93 GeV per nucleon for the solid angle region of the central drift chamber and its surrounding time-of-flight detectors. In order to make the "strange" particles visible in particular, only tracks with momenta of up to 450 MeV/c and velocities of up to 20 cm/ns are accepted. The extremely good resolution enables the detection of negatively-charged kaons, for example, although they are only produced with a relative abundance of 10^-4 per collision. This resolution is independent of the azimuth angle at which the particles are emitted, a fact of decisive importance for the measurement of the correlation of nucleons and kaons discussed in this article.

Due to the conservation of strangeness, at beam energies of less than 2 GeV per nucleon kaons are always produced together with 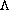-particles. The particles are thus produced at the same location, and interaction with the surrounding matter is responsible for all differences observed in the detector. It therefore follows from the distributions shown in Figure 3, that kaons are repelled from the areas of high baryon density, while -particles are drawn in to these regions. It should, however, be noted that K⁺-mesons, in contrast to the -particles, can leave the reaction volume relatively undisturbed-at least that is what the properties of the free particles seem to indicate. In the lower part of Figure 3, measurements are compared with calculations in which G.Q. Li and C.M. Ko [2] investigated both the free interaction and different versions of the "in-medium interaction" of kaons with the surrounding matter. In the simplest case, corresponding to the dotted line, the kaons should simply not notice the presence of the nucleons. A flow signal in the nucleon direction is to be expected in this case. If an interaction, which can be expressed by a potential, is taken into account, then according to intensity and type, there is agreement with the measured values. The case in which the lateral flow data are described corresponds to the phenomenon of reduced mass mentioned at the start of this section: an attractive scalar potential is required in order to compensate, at least partially, for the strongly repulsive vector potential. Within the context of chiral models, such scalar potentials have clearly-defined effects on the masses of a very wide range of particles

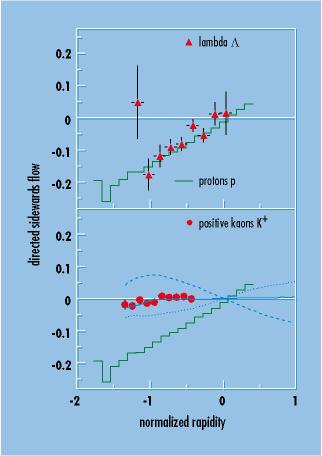
Figure 3: The average values of the projection of the transverse momentum in the reaction plane are shown as a function of the normalized rapidity Y(0), which represents a measure of the velocity along the beam direction. These average values are a measure of the directed sidewards flow. The main flow axis is determined by the protons (green histogram). Differences between the -particles (above) and the positive kaons (below) relative to both themselves and to the protons allow conclusions concerning the interaction with the surrounding medium. One possible explanation in the context of a transport calculation from G.Q. Li and C.M. Ko is offered by the theoretical predictions shown in the diagram for the cases: no potential (dotted), repulsive vector potential (broken line), and scalar and vector potential (continuous line).

In particular, these hypotheses lead to significant differences between K⁺ and K^--mesons, both in the probability of production and in the flow characteristics. However, such investigations are considerably more difficult, as K^--mesons appear less frequently. Such measurements are currently being undertaken, along with the measurement of more exotic, higher-mass particles, such as the 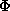-mesons. The first results on the flow characteristics of the antikaons appear to fit with the theoretical predictions of the "chiral" model. However, evaluation is not yet complete. The current FOPI experiment program is expected to produce additional interesting information on the character of the interaction in hot, compressed nuclear matter.

References